这题考构造,难度适中。
首先来说说什么是“度”。
在这里,一个点的“度”指的就是与这个点连接的边的数量。
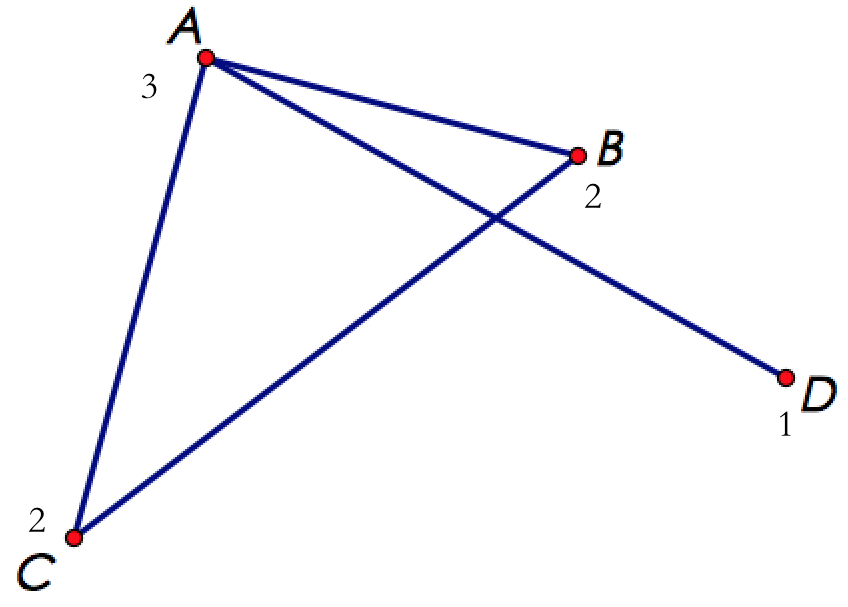
比如下图中,点的度是,点、点的度是,点的度是。
接下来,开始讲题。
本蒟蒻看到题后,第一反应是不会做,第二反应就是拿几组数据试一下,找找规律。
当时,唯一的一个点一定会被删掉,故答案为。
当时,这两个点要么连着,要么分开。连着的时候两个点的度都是,分开的时候两个点的度都是。所以,不管怎样,答案都是。
当时,样例已经解释清楚了,用队列法,答案是。
当时,我们可以试着学学样例,用队列法构造这样的图:

此时,由于没有度为的点,所以外星人会直接删除度为的点,即。
然后图就变成了这样:

此时,外星人应该删除度为的点,但上一步操作使得的度都变成了,外星人无法删除,故幸存了下来。
故答案为二。
难道题目就是想让我们用队列法?当然不是!
当时,如果我们继续用队列法,那么会变成这样:
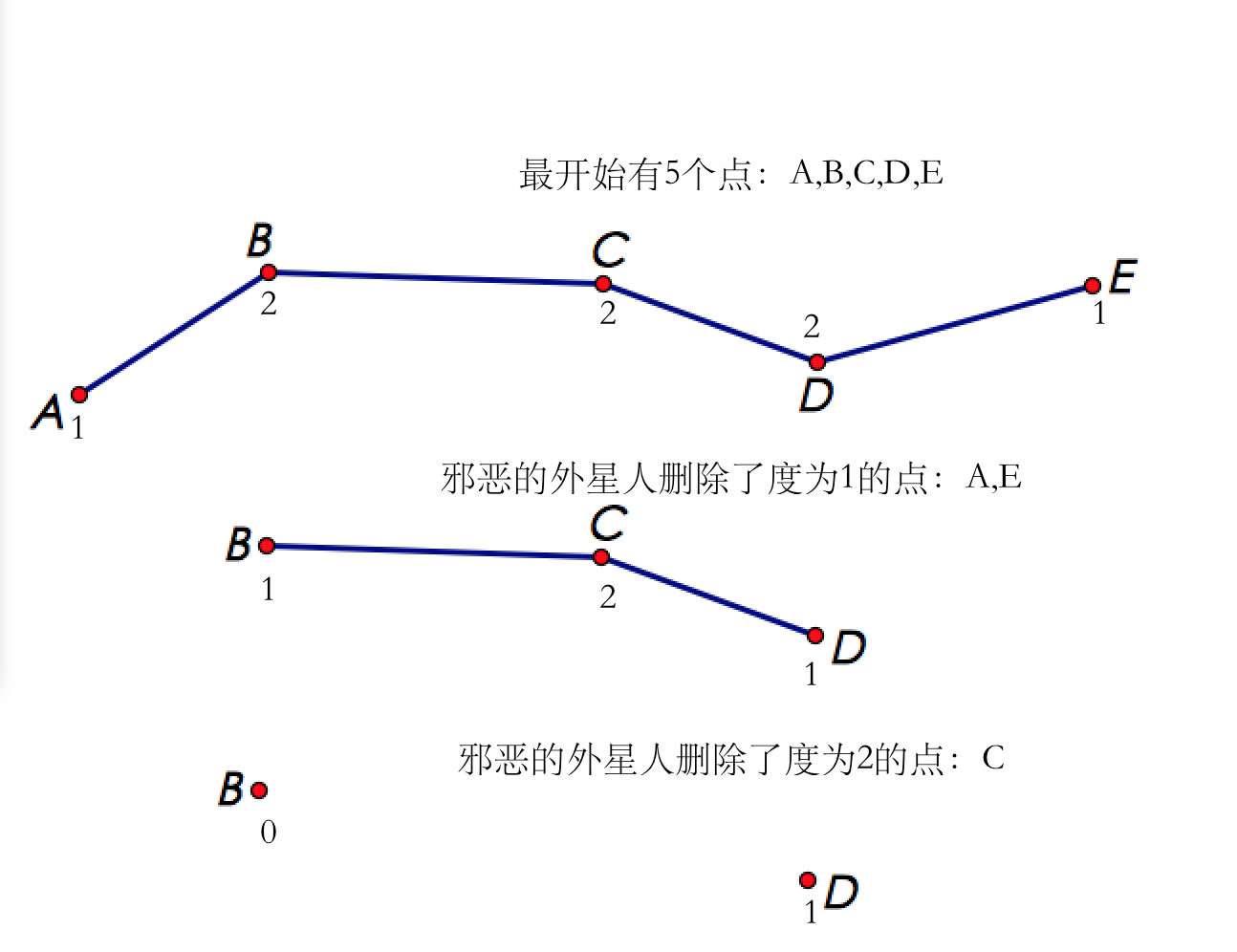
我们惊讶地发现:点居然也被删除了!!!
于是,队列法宣告失败。
不过,在我们前面的枚举中,我们似乎看出了什么端倪:
(下面的表格在题解区有可能会爆,建议去博客区观看。如果表格没爆,请忽略这句话。)
莫非......答案真的是 ?
下面就让我们一起来看一看吧。
以个点为例:
我们先选取两个点,再把与除了彼此之外的所有点相连。
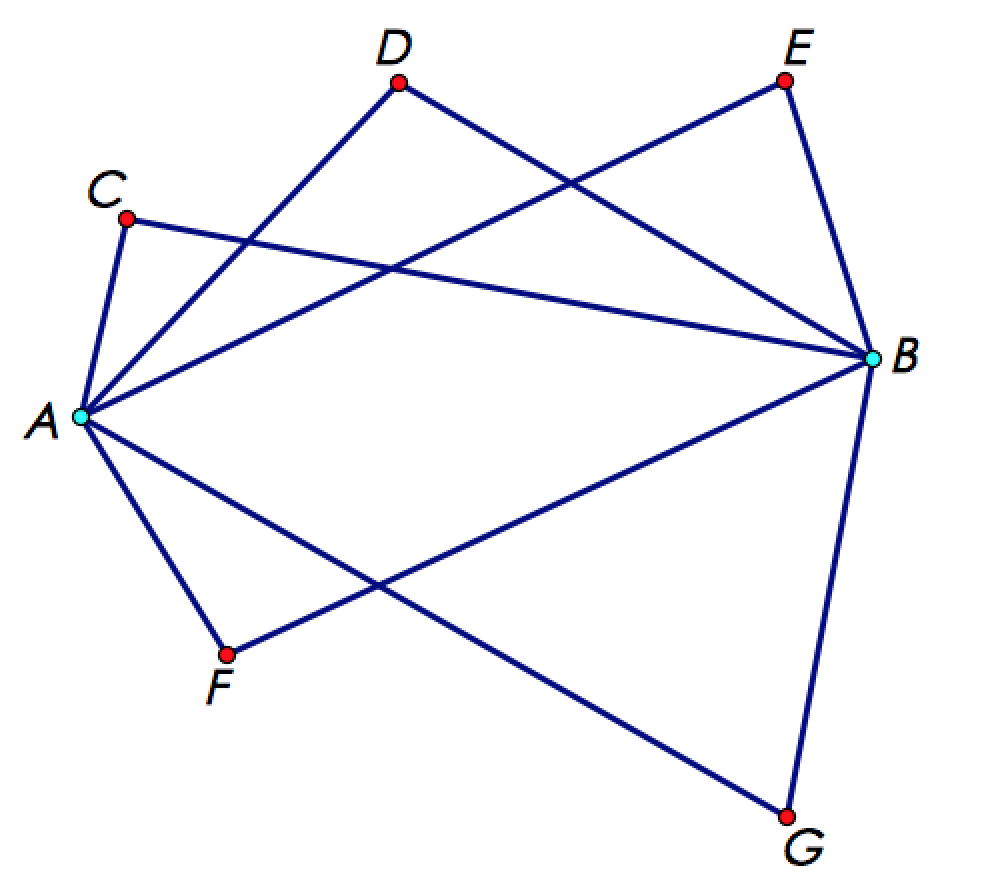
对于剩下的五个点,把每个点与其余的点相连。
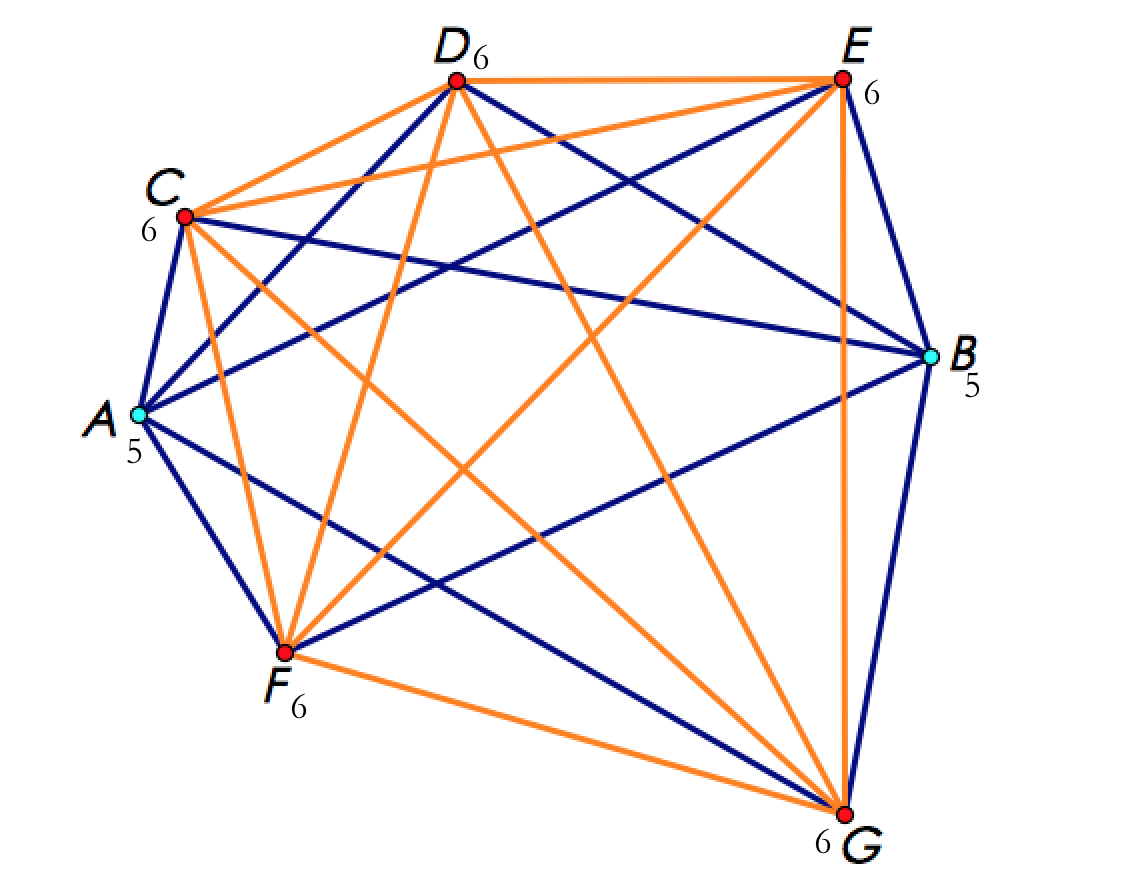
(已经帮各位标过每个点的度了~)
然后,邪恶的外星人删除了度最小的点,即。
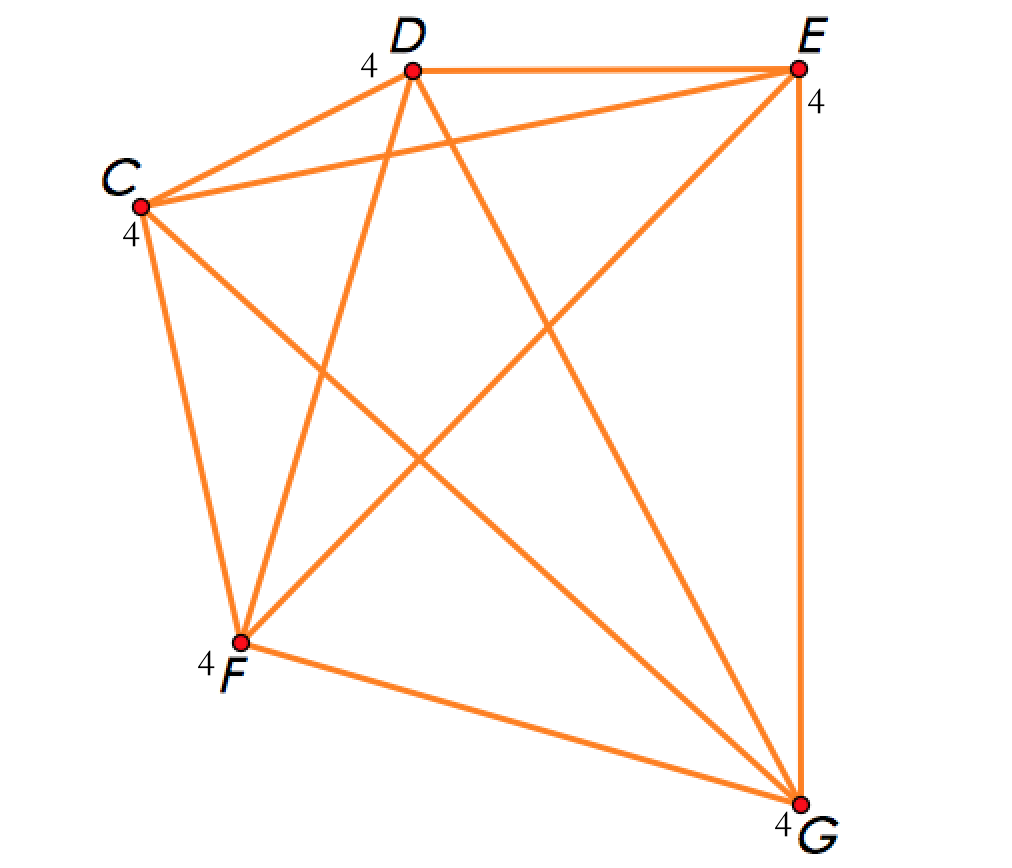
此时,外星人刚刚删除了两个度为的点,应该删除度为的点。
但是删除后,剩下的五个点的度都变成了,外星人无法删除它们,所以这五个点留了下来。
下面证明对于所有情况,都有。
显然,。
假设 ,那么只删除了个点,设为。
由于在个点中,每个点最多只能与除了自身之外所有的点相连,所以每个点的度都不超过。
又,点被删去了,所以点的度小于。
如果删去点影响不到其他点的度,那么必有点的度为。
于是,删去点后,外星人完全可以删去其他的点,这是因为其他点的度一定大于等于,矛盾。
所以删去点必然影响其他点。
又因为外星人只删除了一个点,至多使其他点的度减。
而之前已经说过点的度小于 ,一定存在至少个点与点不相连。(如果与其余点都相连那么点的度就是 了)
又因为点被删去了,所以点的度一定小于其余的点。
所以外星人删去点后,与点不相连的点不受影响,它们的度仍然大于点的度,所以外星人仍然能够继续删除那些与点不相连的点。
所以。
这个之前已经说过构造方法了,是成立的。
所以是合法的解,也是最大的解,所以答案就是。
不过,有一个地方需要注意:当,即时,答案仍然是。
最后,上代码:
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
if(n<2){
cout<<0;
}
else{
cout<<n-2;
}
/*
当然也可以这么写:
cout<<max(0,n-2);
这个语句在n-2<0时自动输出0与n-2中小的那个,而n-2<0,所以会输出0。
*/
return 0;
}
